DETR

End-to-End Object Detection with Transformers [源码] [论文]

DETR是一种基于Transformers的端到端的目标检测模型。

简化了Faster-RCNN、YOLO系列使用proposal-classifier的目标识别流程。

DETR的模型结构非常简单，下图把DETR的所有关键部分全部体现了出来：

  • Backbone
  • Embedding(positional_embeding, query_embeding)
  • Encoder
  • Decoder
  • Feed Forward Network

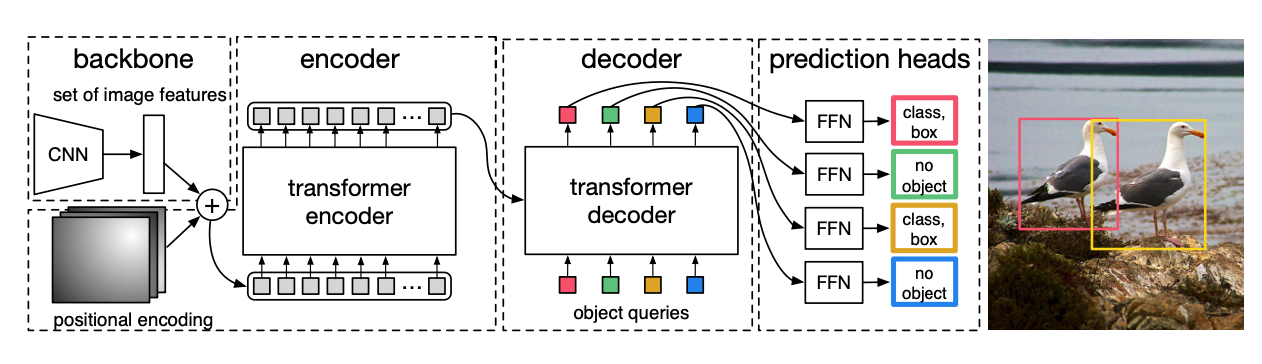
先对模型的前馈流程，以及各个模块的详细组成进行简单介绍。

首先，在图像输入网络前，是需要对其进行尺寸调整的。因为在transformer推理的过程中，需要batch中所有样本的序列长度都一样，所以要把batch的所有图像调整到统一的尺寸。这里会对图像做padding，然后会通过一个mask来记录调整后图像中被padding的位置。mask尺寸为$(bs,H,W)$。

1. Backbone

输入一组图像，张量维度为$(bs,C,H,W)$。

Backbone使用的是Resnet，在经过特征提取后第四个block的输出，分辨率下降16倍，通道数为2048。

将Backbone的输出记为$(bs,2048,h,w)$。

2.Positional Encoding

源码中提供了两种Positional Encoding的方式，这也是目前两种主流的编码方式。

一种使用正余弦编码（相对位置编码），一种可学习的编码方式（绝对位置编码），两种编码方式在最后的结果中并无太大差异，接下来分别对其进行介绍。

2.1 Sinusoidal Position Encoding

在介绍二维的正余弦编码前，可以先回顾一下Attention is all you need 中的一维的正余弦编码。

其编码规则是这样的：

$PE_(pos,2i)=sin(pos/10000^{2i/d_{model}})$

$PE_(pos,2i+1)=cos(pos/10000^{2i/d_{model}})$

其中$pos$表示单词所处句子中的第$pos$个位置，$d_{model}$表示词向量的维度，$i$表示这个词向量的第i维。示例可见上一篇博客

而对于二维的正余弦编码，实际上就是单独对x方向，和单独对y方向编码，然后concat。

接下来通过代码详细解读一下：

1
2
3
4
5
6
7
8
9
10
11
12
# 构建位置编码器，关键参数 N_steps = hidden_dim // 2
def build_position_encoding(args):
    N_steps = args.hidden_dim // 2
    if args.position_embedding in ('v2', 'sine'):
        # TODO find a better way of exposing other arguments
        position_embedding = PositionEmbeddingSine(N_steps, normalize=True)
    elif args.position_embedding in ('v3', 'learned'):
        position_embedding = PositionEmbeddingLearned(N_steps)
    else:
        raise ValueError(f"not supported {args.position_embedding}")

    return position_embedding

有一个关键参数N_steps = hidden_dim // 2，实际上hidden_dim就是输入Transformer中的向量的长度。

因为是将对x和对y方向编码的结果concat到一起，所以这里N_steps就为hidden_dim的一半。

接下来看二维的正余弦编码究竟是如何做的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def forward(self, tensor_list: NestedTensor):
        x = tensor_list.tensors
        mask = tensor_list.mask # (bs, h, w)
        assert mask is not None
        not_mask = ~mask
        y_embed = not_mask.cumsum(1, dtype=torch.float32) # 在维度1的方向上累加
        x_embed = not_mask.cumsum(2, dtype=torch.float32) # 在维度2的方向上累加
        if self.normalize: # 归一化
            eps = 1e-6
            y_embed = y_embed / (y_embed[:, -1:, :] + eps) * self.scale
            x_embed = x_embed / (x_embed[:, :, -1:] + eps) * self.scale
				
        # num_pos_feats = N_steps
        dim_t = torch.arange(self.num_pos_feats, dtype=torch.float32, device=x.device) 
        dim_t = self.temperature ** (2 * (dim_t // 2) / self.num_pos_feats) # (N_steps, )

        pos_x = x_embed[:, :, :, None] / dim_t 
        pos_y = y_embed[:, :, :, None] / dim_t # (bs, h, w, N_steps)
        pos_x = torch.stack((pos_x[:, :, :, 0::2].sin(), pos_x[:, :, :, 1::2].cos()), dim=4).flatten(3) # (bs, h, w, N_steps)
        pos_y = torch.stack((pos_y[:, :, :, 0::2].sin(), pos_y[:, :, :, 1::2].cos()), dim=4).flatten(3) # (bs, h, w, N_steps)
        pos = torch.cat((pos_y, pos_x), dim=3).permute(0, 3, 1, 2) # (bs, h, w, 2*N_steps)
        return pos

直接上图解：

mask $(bs, h , w)$ 中1代表图像padding的位置，0代表的是未经过padding的位置。首先取反的到not_mask，然后在h方向上进行累加，可以的到y_embed，在w方向上进行累加得到x_embed。

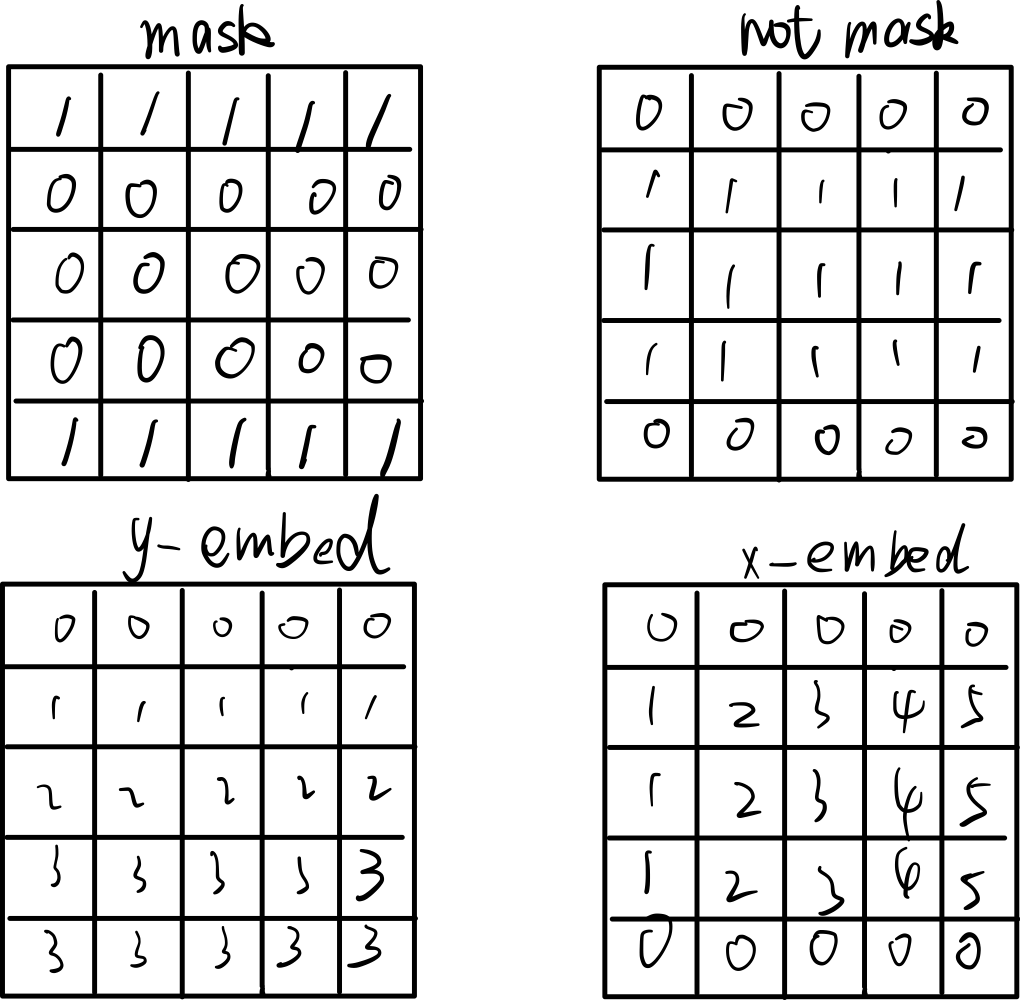
然后进行归一化（表格中的元素还要再乘以scale，scale为$2\pi$）：

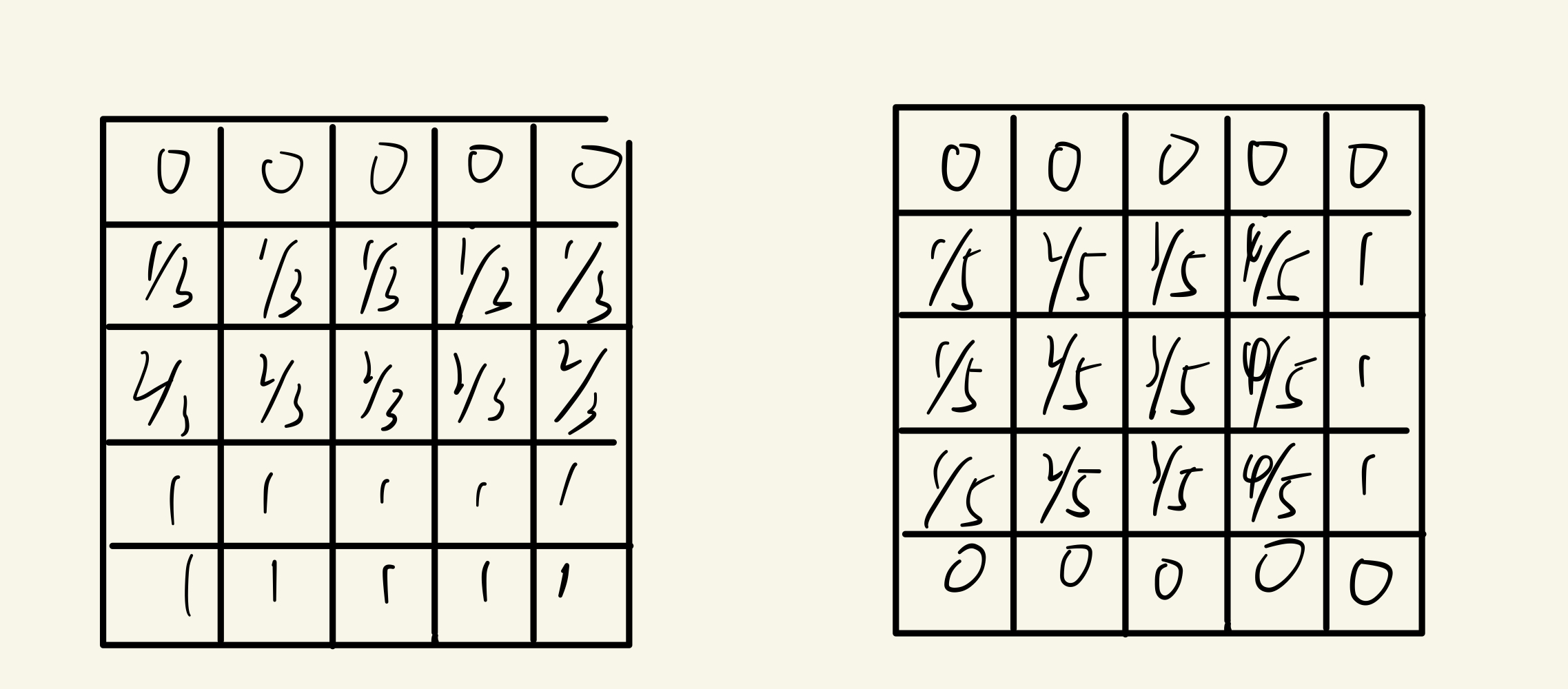
再生成一组dim_t，长度为N_steps。

以N_steps为64为例：$\{10000^{0/64},10000^{0/64},10000^{2/64},10000^{2/64},\dots,10000^{62/64},10000^{62/64}\}$

再将embed$(bs,h,w,1)$除上dim_t，得到pos_x，pos_y($bs, h, w, N_{steps}$)，再进行正弦，余弦操作。

假设N_steps=64，以上图的情况为例，此时pos_y中第3行任意一列对应的位置编码为：

$\{sin(\frac{2}{3}10000^{0/64}), cos(\frac{2}{3}10000^{0/64}), sin(\frac{2}{3}10000^{2/64}), cos(\frac{2}{3}10000^{0/64}), \dots, sin(\frac{2}{3}10000^{62/64}),cos(\frac{2}{3}10000^{62/64})\}$

此时pos_x中第3列的第2，3，4行对应的位置编码为：

$\{sin(\frac{3}{5}10000^{0/64}), cos(\frac{3}{5}10000^{0/64}), sin(\frac{3}{5}10000^{2/64}), cos(\frac{3}{5}10000^{0/64}), \dots, sin(\frac{3}{5}10000^{62/64}),cos(\frac{3}{5}10000^{62/64})\}$

最后对pos_x和pos_y在第4维进行concat操作得到$(bs, h, w, 2N_{steps})$。

最后调整通道方便下一步操作$（bs, 2N_{steps},h,w）$

2.2 Learned Positional Embedding

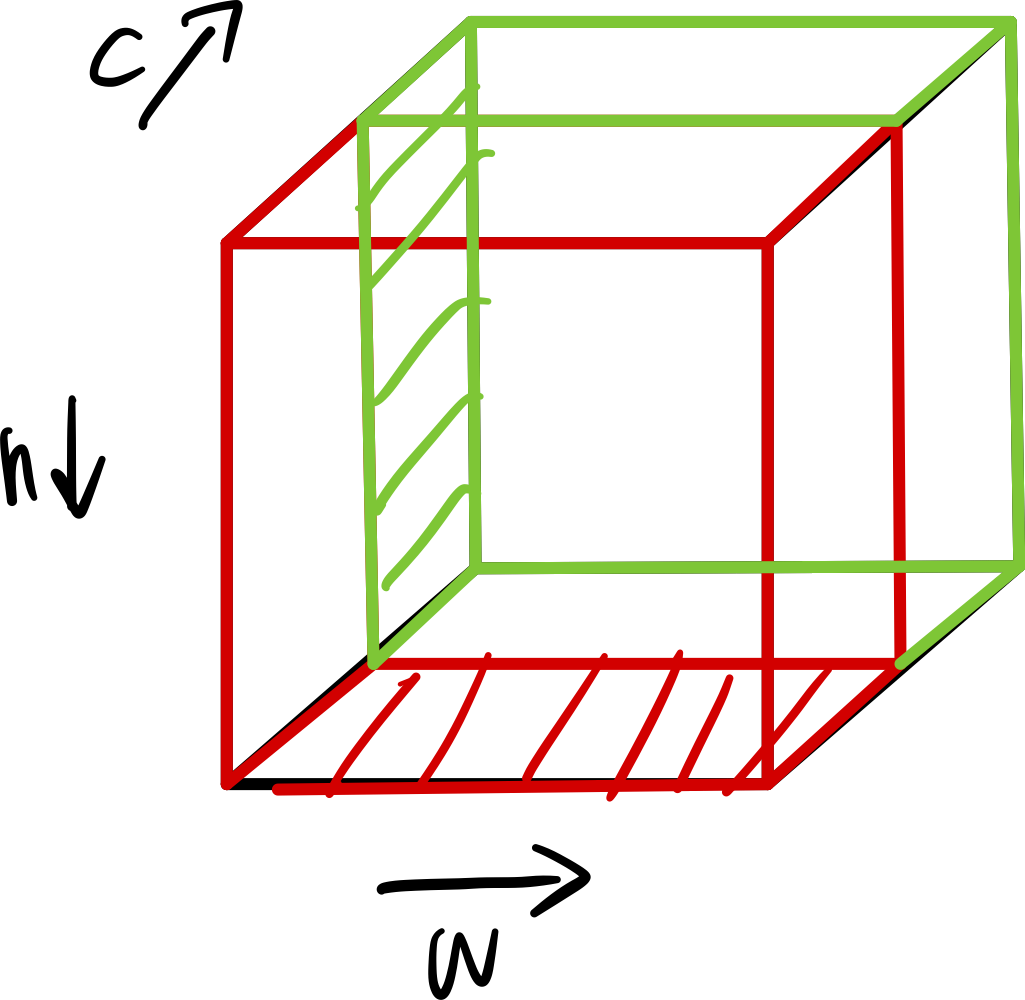
可学习的位置编码相对简单。

图像x尺寸调整后为$(c, h ,w)$，那么直接使用nn.Embedding(50, num_pos_features)对行和列进行随机初始化。

其中num_pos_features = N_steps = hidden_dim // 2。

x_emb：$(w, num_pos_features)$

y_emb：$(h,num_pos_features)$

然后如上图所示，x_emb向h方向复制（红色），y_emb向w方向复制（绿色），得到两个尺寸为$(h, w, num_pos_features)$的张量，再进行concat。

最终得到$(h, w, 2num_pos_features)$。

然后调整通道，方便下一步操作：$(bs, 2num_pos_features,h,w)$。

3 Transformer

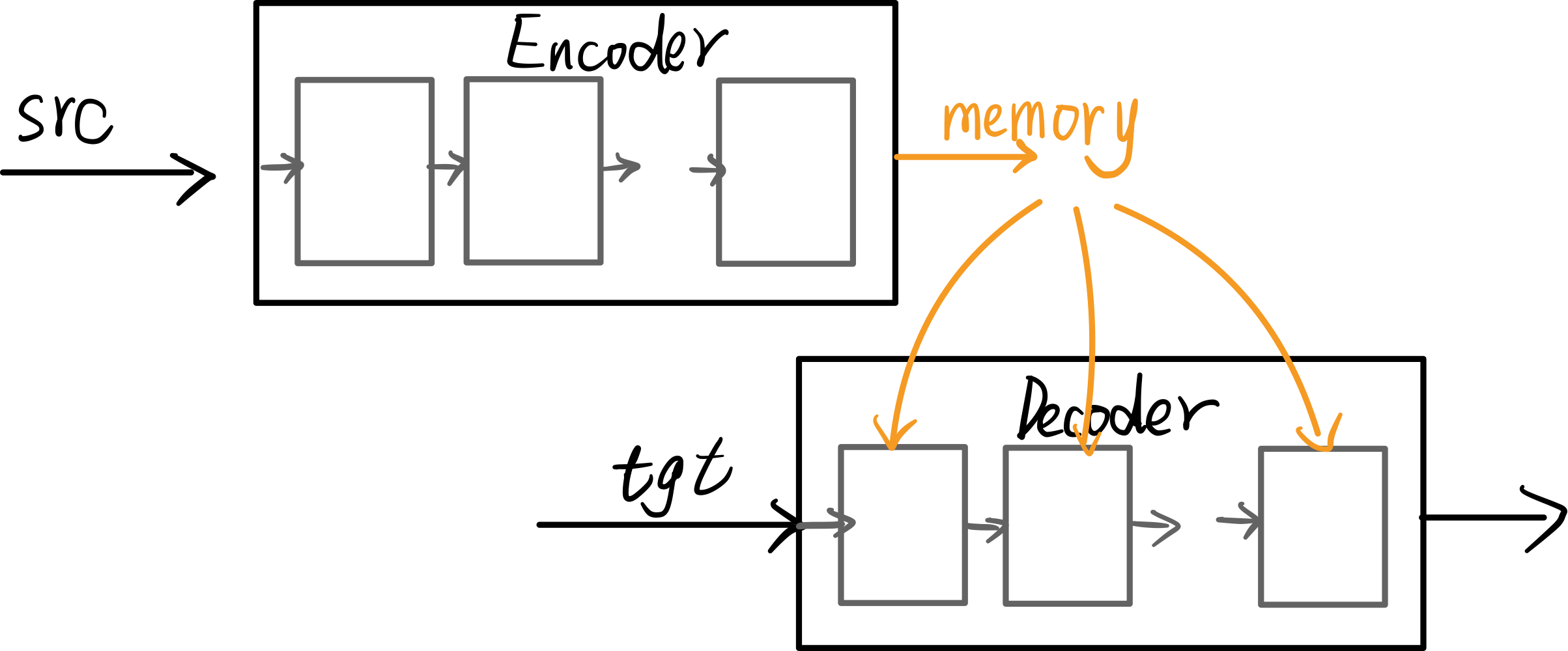
在数据流向Transformer前， 我们已经有了三份数据：

  • 经过backbone提取的特征图：$(bs, c, h, w)$
  • 位置编码：$(bs, hidden_dim, h, w),~hidden_dim=d_model$
  • 图像对应的mask：$(h, w)$

还要第四份数据：query_embeding，作为Decoder的输入，这一步放在Decoder介绍。

这里Transformer的整体结构与Attention is all you need中非常相似，这里主要关注Decoder的输入。

前处理：

Transformer的输入与卷积操作不同，需要对数据的格式进行一些变换。

首先为了降低计算量，减少特征图的通道数：$(bs, 2048, h, w) \to (bs, d_model, h, w) \to (hw, bs, d_model)$

位置编码则也要调整格式：$(bs,d_model,h,w) \to (hw, bs, d_model)$

mask也进行调整：$(h,w)\to(hw, )$

3.1 Encoder Layer

1
2
3
4
5
6
7
8
9
10
11
12
13
14
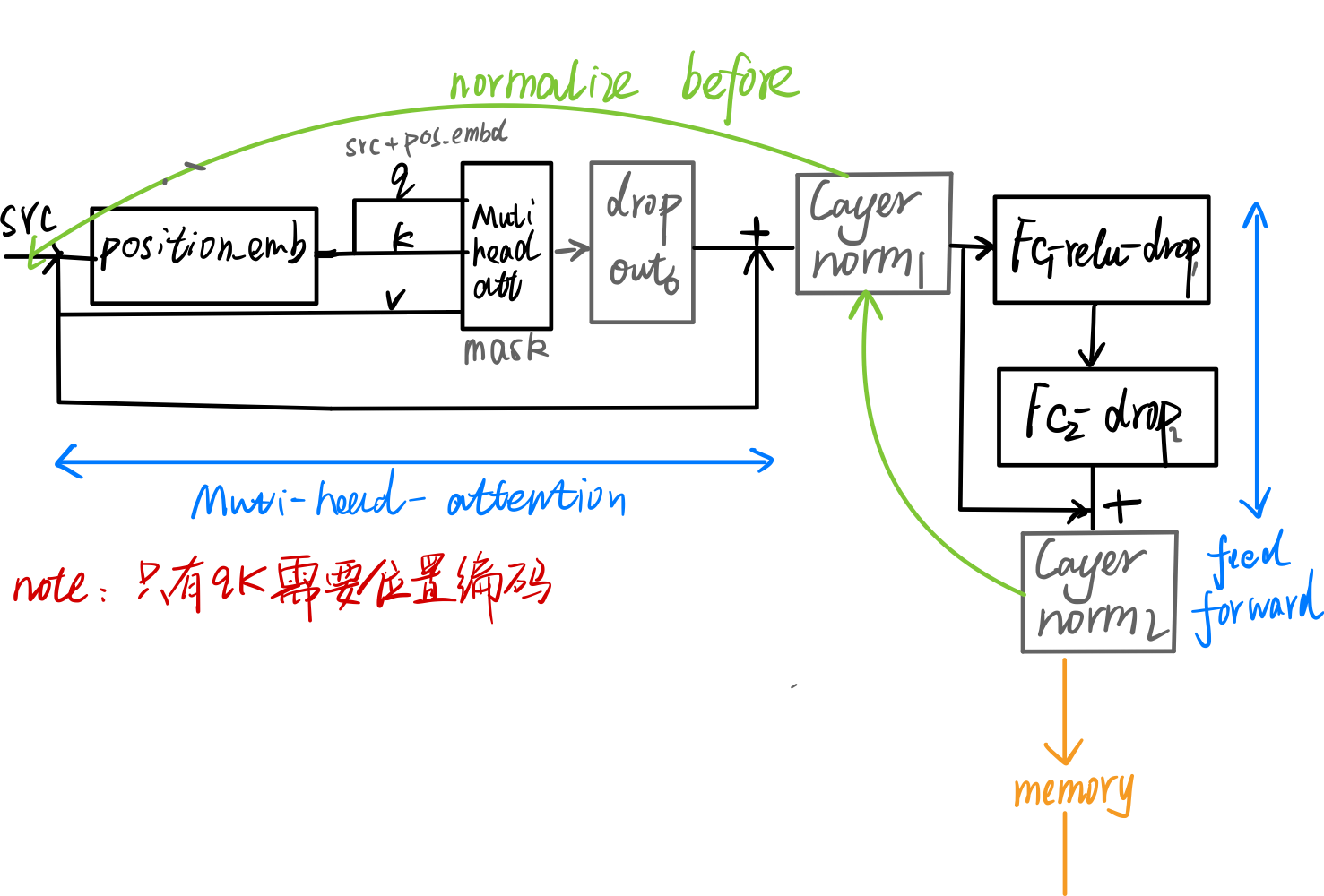
15
def forward_post(self,
                     src,
                     src_mask: Optional[Tensor] = None,
                     src_key_padding_mask: Optional[Tensor] = None,
                     pos: Optional[Tensor] = None):
        q = k = self.with_pos_embed(src, pos) # q = k = src + pos_embed 
        src2 = self.self_attn(q, k, value=src, attn_mask=src_mask,
                              key_padding_mask=src_key_padding_mask)[0]
        src = src + self.dropout1(src2)
        src = self.norm1(src)
        # Feed forward
        src2 = self.linear2(self.dropout(self.activation(self.linear1(src))))
        src = src + self.dropout2(src2)
        src = self.norm2(src)
        return src # (hw, bs , d_model)

Encoder输入的是原图的特征图，输出的尺寸仍然保持不变，相当于每个像素的编码经过self-attention后都引入了其他像素点的信息，建立了原图区域之间的联系。

3.2 Decoder Layer

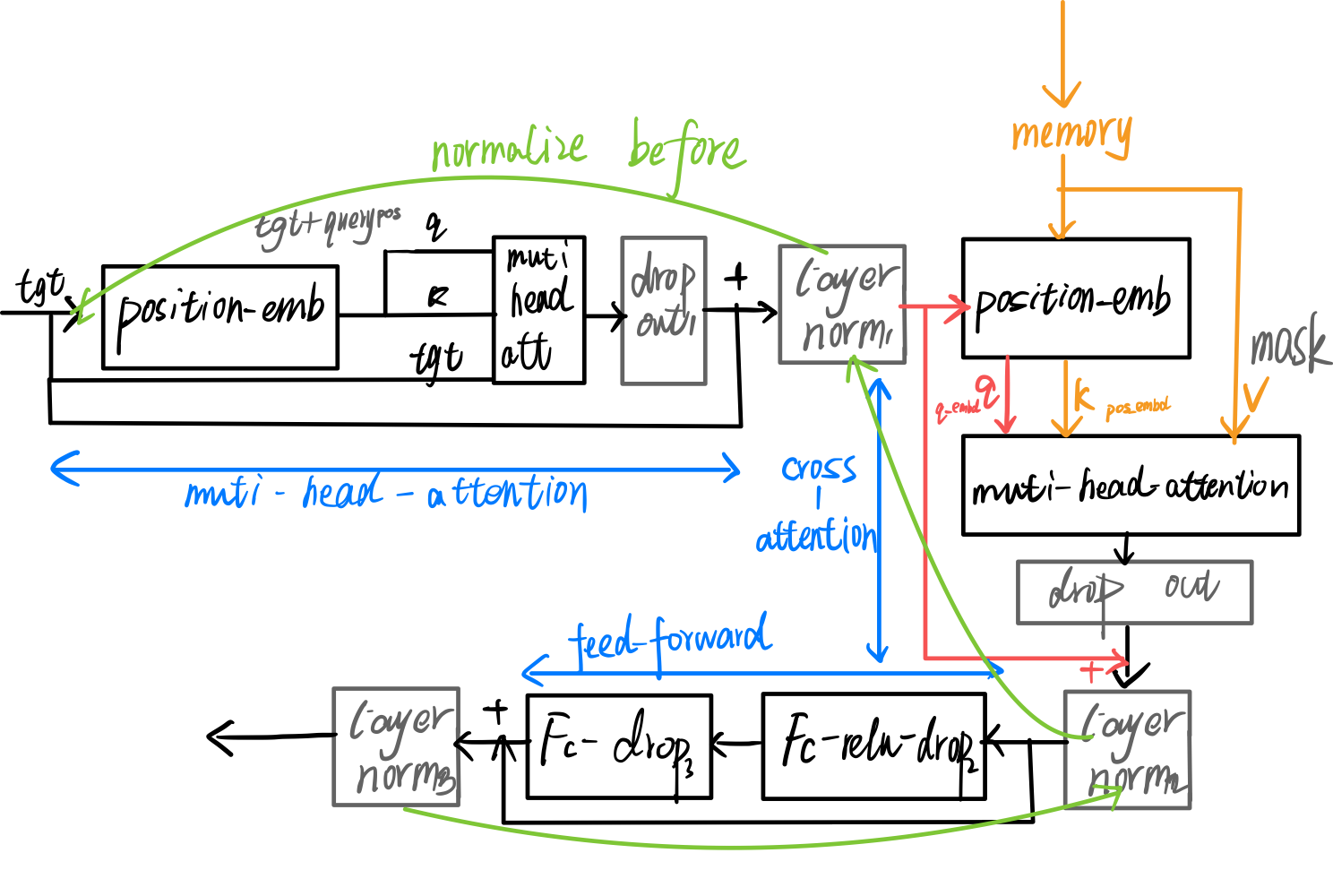
Decoder第一层的输入是一个初始化的维度为$(num_queries,d_model), num_queries=100$的全零张量作为输入。

然后再经过position_embeding，加上一个随初始化，可学习的query_embeding（和初始化的tgt同样尺寸）。

我们知道$Attention(Q,K,V) = Scorefunc(QK)V$

在cross-attention中，$q$来自全零张量，进行通道调整，还加上query_embeding：$(num_queries,bs,d_model)$

$k$来自Encoder的输出加上位置编码：$(hw, bs, d_model)$

$v$来自Encoder的输出：$(hw, bs, d_model)$

通过cross-attention，相当于将$num_queries$个查询，结合encoder输出的特征，得到了$num_queries$个目标。

最后Deocder的输出为$(num_queries, bs, d_model)$

4. FeedForward

最后接两组并行的全联接层，一组输出每个query对应的得分情况，一组输出每个query对应的bbox。